MATRIX
Numbers 18:15
Viewing the 1769 King James Version. Click to switch to 1611 King James Version of Numbers 18:15Every thing that openeth the matrix in all flesh, which they bring unto the LORD, [whether it be] of men or beasts, shall be thine: nevertheless the firstborn of man shalt thou surely redeem, and the firstling of unclean beasts shalt thou redeem.
In mathematics, a matrix (plural matrices, or less commonly matrixes) is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements is
Matrices of the same size can be added or subtracted element by element. The rule for matrix multiplication
is more complicated, and two matrices can be multiplied only when the
number of columns in the first equals the number of rows in the second. A
major application of matrices is to represent linear transformations, that is, generalizations of linear functions such as f(x) = 4x. For example, the rotation of vectors in three dimensional space is a linear transformation. If R is a rotation matrix and v is a column vector (a matrix with only one column) describing the position of a point in space, the product Rv
is a column vector describing the position of that point after a
rotation. The product of two matrices is a matrix that represents the composition of two linear transformations. Another application of matrices is in the solution of a system of linear equations. If the matrix is square, it is possible to deduce some of its properties by computing its determinant. For example, a square matrix has an inverse if and only if its determinant is not zero. Eigenvalues and eigenvectors provide insight into the geometry of linear transformations.
Matrices find applications in most scientific fields. In physics, matrices are used to study electrical circuits, optics, and quantum mechanics. In computer graphics, matrices are used to project a 3-dimensional image onto a 2-dimensional screen, and to create realistic-seeming motion. Matrix calculus generalizes classical analytical notions such as derivatives and exponentials to higher dimensions.

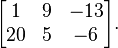


Comments
Post a Comment